My wife tells me my blog is boring because it doesn’t have enough pictures…and also it’s about accounting. So, with that in mind, I am prepared to blow your mind with this post, pictures and all. Benford’s Law. Who’s heard of it? Anybody. Anybody. Bueller…. This is Benford’s Law.
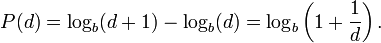
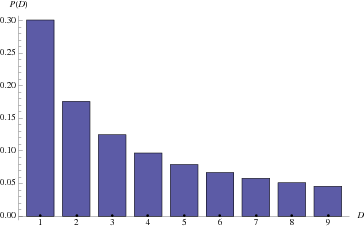
What, equations don’t do it for you? Well then, let’s dive in. Benford’s Law is one of those things that can be proven mathematically, but flies in the face of common sense. People have tried to explain the mechanics, but to me it’s like gravity. Nobody really understands it. We just know it works. It states that in large, non-standard, real life tables of numbers (i.e. water bills, death rates, bank amounts), there is a pattern. Sounds very ominous doesn’t it? For any given dataset, 1 is the first digit around 30% of the time. Subsequent leading digits appear in descending probability, with 9 occurring as the first digit less than 5% of the time. Here’s a picture (for you honey).
[
This has all sorts of implications in the real world. It means that if you take a large enough dataset and compare the leading digits to Benford’s Law, there should be a close match. If not, it is likely that human tampering of the data has occurred. This is one of the tests that gives auditors the warm-fuzzies. Fraudsters, when they tamper with data, tend to use the same leading digit or a random assortment of leading digits. For example, say you have an evil staff accountant who makes a large number of small dollar revenue entries that, when aggregated, inflate revenue by a material amount. Normal substantive tests may not catch this fraud because each entry by itself is immaterial. However, because people tend to reuse leading digits in repetitive tasks, the clerk’s entries likely would cause the data not to conform to Benford’s law, thus allowing the auditor to identify the fraud. Well, that’s all I’ve got for tonight. I’m glad we could have this talk.